Leading-order Term on:
[Wikipedia]
[Google]
[Amazon]
The leading-order terms (or corrections) within a
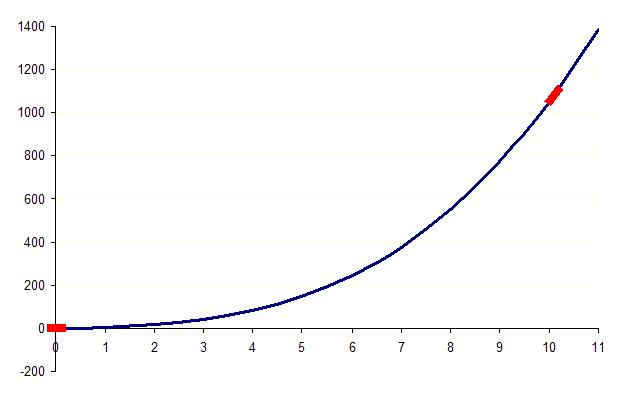 Suppose we want to understand the leading-order behaviour of the example above.
*When ''x'' = 0.001, the ''x''3 and 5''x'' terms may be regarded as negligible, and dropped, along with any values in the third decimal places onwards in the two remaining terms. This gives the leading-order balance ''y'' = 0.1. Thus the leading-order behaviour of this equation at ''x=0.001'' is that ''y'' is constant.
*Similarly, when ''x'' = 10, the 5''x'' and 0.1 terms may be regarded as negligible, and dropped, along with any values in the third significant figure onwards in the two remaining terms. This gives the leading-order balance ''y'' = ''x''3. Thus the leading-order behaviour of this equation at ''x=10'' is that ''y'' increases cubically with ''x''.
The main behaviour of ''y'' may thus be investigated at any value of ''x''. The leading-order behaviour is more complicated when more terms are leading-order. At ''x=2'' there is a leading-order balance between the cubic and linear dependencies of ''y'' on ''x''.
Note that this description of finding leading-order balances and behaviours gives only an outline description of the process – it is not mathematically rigorous.
Suppose we want to understand the leading-order behaviour of the example above.
*When ''x'' = 0.001, the ''x''3 and 5''x'' terms may be regarded as negligible, and dropped, along with any values in the third decimal places onwards in the two remaining terms. This gives the leading-order balance ''y'' = 0.1. Thus the leading-order behaviour of this equation at ''x=0.001'' is that ''y'' is constant.
*Similarly, when ''x'' = 10, the 5''x'' and 0.1 terms may be regarded as negligible, and dropped, along with any values in the third significant figure onwards in the two remaining terms. This gives the leading-order balance ''y'' = ''x''3. Thus the leading-order behaviour of this equation at ''x=10'' is that ''y'' increases cubically with ''x''.
The main behaviour of ''y'' may thus be investigated at any value of ''x''. The leading-order behaviour is more complicated when more terms are leading-order. At ''x=2'' there is a leading-order balance between the cubic and linear dependencies of ''y'' on ''x''.
Note that this description of finding leading-order balances and behaviours gives only an outline description of the process – it is not mathematically rigorous.
Cornell University notes
/ref> Also, the thin film equations of
mathematical
Mathematics is an area of knowledge that includes the topics of numbers, formulas and related structures, shapes and the spaces in which they are contained, and quantities and their changes. These topics are represented in modern mathematics ...
equation
In mathematics, an equation is a formula that expresses the equality of two expressions, by connecting them with the equals sign . The word ''equation'' and its cognates in other languages may have subtly different meanings; for example, in ...
, expression
Expression may refer to:
Linguistics
* Expression (linguistics), a word, phrase, or sentence
* Fixed expression, a form of words with a specific meaning
* Idiom, a type of fixed expression
* Metaphorical expression, a particular word, phrase, o ...
or model
A model is an informative representation of an object, person or system. The term originally denoted the Plan_(drawing), plans of a building in late 16th-century English, and derived via French and Italian ultimately from Latin ''modulus'', a mea ...
are the terms with the largest order of magnitude
An order of magnitude is an approximation of the logarithm of a value relative to some contextually understood reference value, usually 10, interpreted as the base of the logarithm and the representative of values of magnitude one. Logarithmic dis ...
.J.K.Hunter, ''Asymptotic Analysis and Singular Perturbation Theory'', 2004. http://www.math.ucdavis.edu/~hunter/notes/asy.pdf The sizes of the different terms in the equation(s) will change as the variables change, and hence, which terms are leading-order may also change.
A common and powerful way of simplifying and understanding a wide variety of complicated mathematical models is to investigate which terms are the largest (and therefore most important), for particular sizes of the variables and parameters, and analyse the behaviour produced by just these terms (regarding the other smaller terms as negligible). This gives the main behaviour – the true behaviour is only small deviations away from this. This main behaviour may be captured sufficiently well by just the strictly leading-order terms, or it may be decided that slightly smaller terms should also be included. In which case, the phrase leading-order terms might be used informally to mean this whole group of terms. The behaviour produced by just the group of leading-order terms is called the leading-order behaviour of the model.
Basic example
Consider the equation ''y'' = ''x''3 + 5''x'' + 0.1. For five different values of ''x'', the table shows the sizes of the four terms in this equation, and which terms are leading-order. As ''x'' increases further, the leading-order terms stay as ''x''3 and ''y'', but as ''x'' decreases and then becomes more and more negative, which terms are leading-order again changes. There is no strict cut-off for when two terms should or should not be regarded as ''approximately'' the same order, or magnitude. One possiblerule of thumb
In English, the phrase ''rule of thumb'' refers to an approximate method for doing something, based on practical experience rather than theory. This usage of the phrase can be traced back to the 17th century and has been associated with various t ...
is that two terms that are within a factor of 10 (one order of magnitude) of each other should be regarded as of about the same order, and two terms that are not within a factor of 100 (two orders of magnitude) of each other should not. However, in between is a grey area, so there are no fixed boundaries where terms are to be regarded as approximately leading-order and where not. Instead the terms fade in and out, as the variables change. Deciding whether terms in a model are leading-order (or approximately leading-order), and if not, whether they are small enough to be regarded as negligible, (two different questions), is often a matter of investigation and judgement, and will depend on the context.
Leading-order behaviour
Equations with only one leading-order term are possible, but rare. For example, the equation 100 = 1 + 1 + 1 + ... + 1, (where the right hand side comprises one hundred 1's). For any particular combination of values for the variables and parameters, an equation will typically contain at least two leading-order terms, and other lower-order terms. In this case, by making the assumption that the lower-order terms, and the parts of the leading-order terms that are the same size as the lower-order terms (perhaps the second or thirdsignificant figure
Significant figures (also known as the significant digits, ''precision'' or ''resolution'') of a number in positional notation are digits in the number that are reliable and necessary to indicate the quantity of something.
If a number expre ...
onwards), are negligible, a new equation may be formed by dropping all these lower-order terms and parts of the leading-order terms. The remaining terms provide the leading-order equation, or leading-order balance, or dominant balance, and creating a new equation just involving these terms is known as ''taking an equation to leading-order''. The solutions to this new equation are called the leading-order solutions to the original equation. Analysing the behaviour given by this new equation gives the leading-order behaviour of the model for these values of the variables and parameters. The size of the error in making this approximation is normally roughly the size of the largest neglected term.
Next-to-leading order
Of course, ''y'' is not ''actually'' completely constant at ''x'' = 0.001 – this is just its main behaviour in the vicinity of this point. It may be that retaining only the leading-order (or approximately leading-order) terms, and regarding all the other smaller terms as negligible, is insufficient (when using the model for future prediction, for example), and so it may be necessary to also retain the set of next largest terms. These can be called the next-to-leading order (NLO) terms or corrections. The next set of terms down after that can be called the next-to-next-to-leading order (NNLO) terms or corrections.Usage
Matched asymptotic expansions
Leading-order simplification techniques are used in conjunction with themethod of matched asymptotic expansions In mathematics, the method of matched asymptotic expansions is a common approach to finding an accurate approximation to the solution to an equation, or system of equations. It is particularly used when solving singularly perturbed differential eq ...
, when the accurate approximate solution in each subdomain is the leading-order solution.{{Cite journal , last=Kivshar , first=Y.S. , year=1998 , title=Dynamics of optical vortex solitons , url=http://wwwrsphysse.anu.edu.au/nonlinear/papers/pdf/OC_1998_152_00198.pdf , archive-url=https://web.archive.org/web/20130421144048/http://wwwrsphysse.anu.edu.au/nonlinear/papers/pdf/OC_1998_152_00198.pdf , archive-date=2013-04-21 , journal=Optics Communications , volume=152 , issue=1 , pages=198–206 , doi=10.1016/S0030-4018(98)00149-7 , bibcode=1998OptCo.152..198K , display-authors=etal , access-date=2012-10-31 , url-status=dead
Simplifying the Navier–Stokes equations
For particular fluid flow scenarios, the (very general)Navier–Stokes equations
In physics, the Navier–Stokes equations ( ) are partial differential equations which describe the motion of viscous fluid substances, named after French engineer and physicist Claude-Louis Navier and Anglo-Irish physicist and mathematician Geo ...
may be considerably simplified by considering only the leading-order components. For example, the Stokes flow
Stokes flow (named after George Gabriel Stokes), also named creeping flow or creeping motion,Kim, S. & Karrila, S. J. (2005) ''Microhydrodynamics: Principles and Selected Applications'', Dover. . is a type of fluid flow where advective iner ...
equations./ref> Also, the thin film equations of
lubrication theory
In fluid dynamics, lubrication theory describes the flow of fluids (liquids or gases) in a geometry in which one dimension is significantly smaller than the others. An example is the flow above air hockey tables, where the thickness of the air ...
.
See also
* Valuation, an algebraic generalization of "leading order"References